Generate Encryption Key With Diffie Hellman
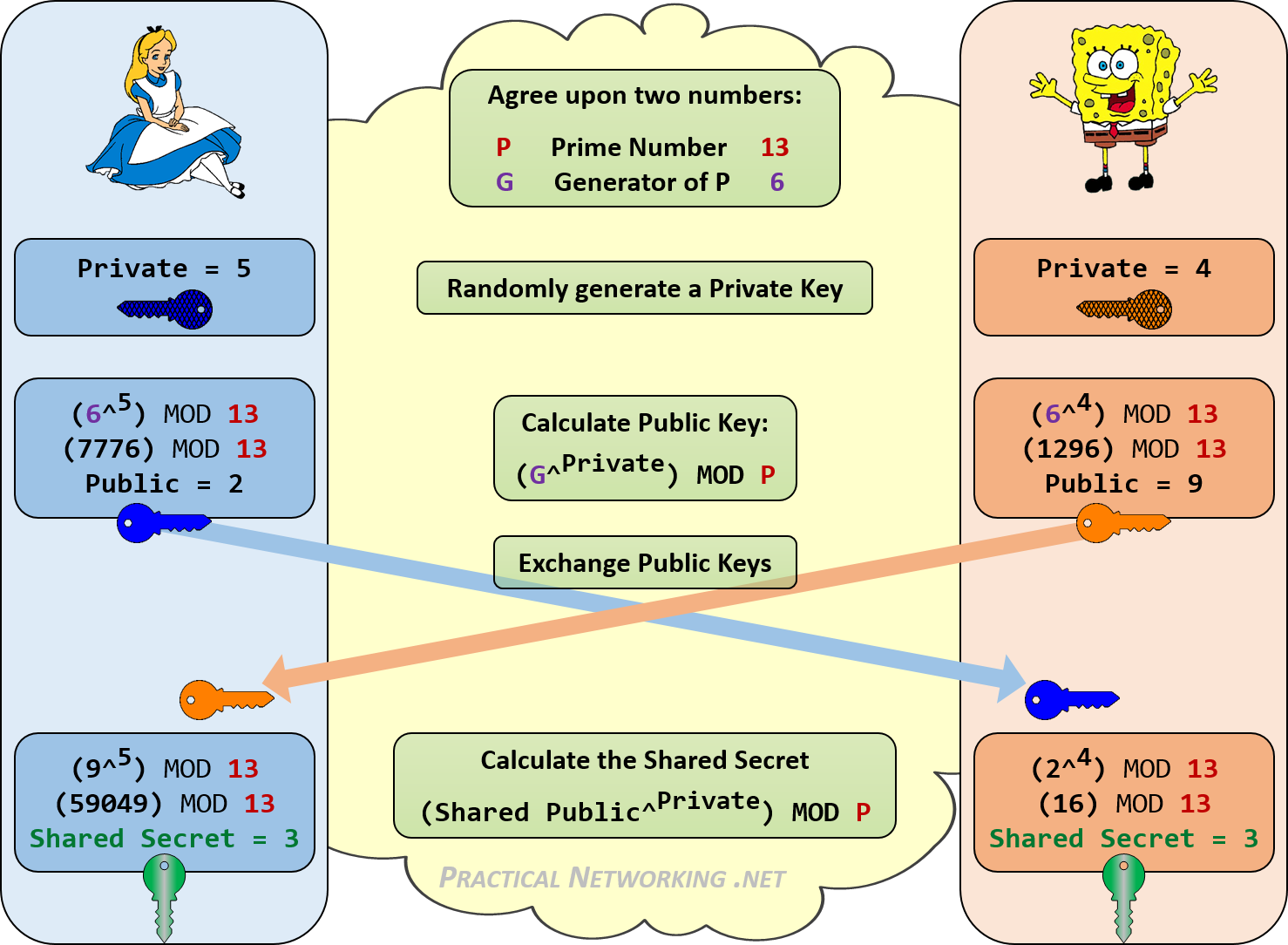
I'm trying to implement a diffie-hellman key exchange. Let's say I found a large prime number p - how can I find a generator g? Restricted by the multiprecision library that I have to use, only a few basic operations (+,., -, /, pow, modExp, modMult, mod, gcd, isPrime, genRandomPrime, genRandomBits, and a few more) are available. 2018-7-21 Diffie-Hellman Key Exchange. One of the brute approaches for secure transfer can be that user A can encrypt the using a key and later the key could be shared with user B. This approach can work up to an extent but it always has a risk of third-party eavesdroppping. We needed a system in which two users, without knowing the secret key, can. 2020-3-26 Before we start into looking into the issue it might be a good idea to reiterate how these schemes work. We will start with a very naive and insecure version of the Diffie-Hellman-Key-Exchange (DH-KX) and improve it from there, After that we will take a short look at ElGamal-Encryption. Walkthrough of Diffie-Hellman Key Exchange. We can say it's practically impossible for her to break the encryption in a reasonable amount of time. This solves the.
- Generate Encryption Key With Diffie Hellman Windows 10
- Generate Encryption Key With Diffie Hellman Texas
- Generate Encryption Key With Diffie Hellman Free
- Wireshark Diffie Hellman
- Generate Encryption Key With Diffie Hellman Lyrics
- Openssl Diffie Hellman
Public-Key Cryptography and Diffie-Hellman Certificates
Public-Private Keys
Cryptography takes the original message, and produces an encoded version by using a special piece of information known to the sender and receiver. The original message is called the plaintext, the special information is called the key, and the resulting message is called the ciphertext. Cryptosystems work by taking the digital representation of the plaintext and manipulating it mathematically under the control of the digital key to produce the ciphertext.
Public-key cryptography was invented by Whitfield Diffie and Martin Hellman. It takes a message encrypted in one shared secret and decrypts it in another. The keys are mathematically related in such a way that a knowledge of one key does not make it possible to figure out the other key. This permits the one key, the public key, to be made widely known, while the corresponding private key is known only to a single user. The two keys together are called a key pair.
The Diffie-Hellman key produces shared secret keys directly from private and public components that are not in themselves keys. The advantage of a public-key system is that the secret components do not have to be shared to exchange information securely. The private portion is never given out to anyone, and it cannot feasibly be calculated from the public portion.
Certificates
To know that the key pair being used in the transaction is actually the key pair for that user, a special sort of signed record is used called a certificate. A certificate contains information identifying the user: distinguished name, public key, and expiration date; for example, digitally signed by a trusted network entity called a certification authority (CA).
Certification Authority
The CA's public key is known to every user of the network. This permits anyone wishing to authenticate a certificate to follow the same procedure for authenticating a message. The CA's public key is available in certificate format so that it, too, can be verified. The major commercial application for CAs is to authenticate businesses and the employees of those businesses. SunCA and SunCAglobal are Sun Microsystems' certification authority in the Internet Commerce Group (ICG).
Unsigned Diffie-Hellman (UDH) Keys
Unsigned Diffie-Hellman (UDH) keys derive their certificate name from the hash of the public key. By communicating the hash over the telephone or some other trusted method of communication with another party, user's can securely communicate without requiring the infrastructure of a CA. How their certificate name is derived and how this is placed in the SKIP packet are shown in Figure B-4.
Figure B-4 Unsigned Diffie-Hellman Keys
The advantages of UDH pairs of public and private keys over signed certificates are as follows:
The private key is a 256-bit secret that is generated by the user. This secret never leaves the user's machine so there is no longer any need to keep the floppy diskettes containing the certificate locked up somewhere nor to trust that the packages have not been tampered with. All that is necessary is to trust that the user's machine is kept secure.
Since the private key is always in the user's machine, the physical handling of the key is eliminated so there is no need for a CA and no need to package and ship the private keys.
Since a key cannot be duplicated and is not registered by a CA, it does not need to be formally revoked; if there is reason to believe a key has been compromised, just generate a new key and repeat the distribution and authentication of your public value and its ID.
The authentication of the public keys is simplified because it does not have to be done secretly, merely securely.
An example of this last point might be as follows: Two users call each other on the telephone and exchange public keys using the recognition of each other's voice as the authentication mechanism. Because these are hashes of public keys, it does not matter if anyone overhears the conversation.
The disadvantage of UDH keys is that the names must be communicated out of band, such as over the telephone by PGP.
SKIP must be able to name or identify a given key. It does this by using a name or identifier drawn from a namespace identifier (NSID). It also must be able to figure out which certificate name to use when communicating with a remote system. This information can be derived from its IP address or explicitly stated in the protocol via NSID/key ID.
If NSID is set to 0, the IP address is used for key lookup. By default, the NSID is set at 0 and a key ID is not sent; however, with the key ID feature activated, key names are no longer tied to IP addresses. This means that regardless of their physical location on the network or on the Internet, various people have the ability to communicate with each other and corporate using encryption.
The Namespace Identifiers (NSID)
SunScreen SKIP provides users with the ability to separate the identity of an entity from its physical address. This means that each person (sender or receiver) participating in a transfer of encrypted data over a computer network can be identified by a namespace identifier/key identifier (NSID/key ID) pair.
NSIDs are a part of SKIP; these identifiers are used to identify the keys being used. The NSIDs supported by SunScreen SKIP are
NSID 0 (No Key ID present, figure out which key to use from the IP address)
NSID 1 (IPv4 address key ID, for hosts whose key IDs do not match their IP address, such as hosts that use signed SunCA keys)
NSID 8 (MD5 hash of Diffie-Hellman Public Value Key ID present, for UDH keys that are not signed by any CA)
The first two are nearly identical in that they both use signed X.509 keys, with one very important difference. SKIP packets that use NSID 1 include the key ID in the packet. SKIP packets that use NSID 0 figure out which key to use.
With SunCA keys, for example, it is necessary to put the key identifier into the SKIP header because the IP address may not correspond to the identifier in the certificate. If there is a SunCA key identifier of '0a000101' for a certificate, it becomes '10.0.1.1' in IP address terminology.
Further, if your IP address is '192.12.10.49,' then you would have to include your key identifier in the SKIP header because it does not equal your IP address. But with NSID 0, which also uses X.509 certificates, it is guaranteed that the key identifier is the IP address; therefore, the key identifier does not have to be sent.
Using NSID 0 results in a small gain in efficiency by not having to send the key identifier. This is what is meant by 'No Key ID present' in the NSID 0 bullet above. This approach reduces the amount of packet expansion because of SKIP.
Traffic Encryption
Traffic is encrypted using conventional symmetric key cryptography, such as RC2, RC4, DES, and the like. The user installs SunScreen SKIP, which has the algorithm packages that are required. Traffic encryption keys are changed based on the volume of data and the length of time a key is used.
There is a tool with a GUI to control how often you want the traffic encryption keys changed. As shipped, the default is to change traffic keys after every 512K bytes of data or after being used for 30 seconds; traffic keys are deleted after being unused for 30 seconds. You can change these values to meet the security needs of your site. This tool is discussed in detail in Chapter 3.
It is important to change the traffic encryption keys frequently enough so that cracking a key will leave little data, and yet not so frequently so that reconfiguring the keys incurs excessive overhead.
- Cryptography Tutorial
- Cryptography Useful Resources
- Selected Reading
Public Key Cryptography
Unlike symmetric key cryptography, we do not find historical use of public-key cryptography. It is a relatively new concept.
Symmetric cryptography was well suited for organizations such as governments, military, and big financial corporations were involved in the classified communication.
With the spread of more unsecure computer networks in last few decades, a genuine need was felt to use cryptography at larger scale. The symmetric key was found to be non-practical due to challenges it faced for key management. This gave rise to the public key cryptosystems.
The process of encryption and decryption is depicted in the following illustration −
The most important properties of public key encryption scheme are −
Different keys are used for encryption and decryption. This is a property which set this scheme different than symmetric encryption scheme.
Each receiver possesses a unique decryption key, generally referred to as his private key.
Receiver needs to publish an encryption key, referred to as his public key.
Some assurance of the authenticity of a public key is needed in this scheme to avoid spoofing by adversary as the receiver. Generally, this type of cryptosystem involves trusted third party which certifies that a particular public key belongs to a specific person or entity only.
Encryption algorithm is complex enough to prohibit attacker from deducing the plaintext from the ciphertext and the encryption (public) key.
Though private and public keys are related mathematically, it is not be feasible to calculate the private key from the public key. In fact, intelligent part of any public-key cryptosystem is in designing a relationship between two keys.
There are three types of Public Key Encryption schemes. We discuss them in following sections −
RSA Cryptosystem
This cryptosystem is one the initial system. It remains most employed cryptosystem even today. The system was invented by three scholars Ron Rivest, Adi Shamir, and Len Adleman and hence, it is termed as RSA cryptosystem.
We will see two aspects of the RSA cryptosystem, firstly generation of key pair and secondly encryption-decryption algorithms.
Generation of RSA Key Pair
Each person or a party who desires to participate in communication using encryption needs to generate a pair of keys, namely public key and private key. The process followed in the generation of keys is described below −
Generate the RSA modulus (n)
Select two large primes, p and q.
Calculate n=p*q. For strong unbreakable encryption, let n be a large number, typically a minimum of 512 bits.
Find Derived Number (e)
Number e must be greater than 1 and less than (p − 1)(q − 1).
There must be no common factor for e and (p − 1)(q − 1) except for 1. In other words two numbers e and (p – 1)(q – 1) are coprime.
Form the public key
The pair of numbers (n, e) form the RSA public key and is made public.
Interestingly, though n is part of the public key, difficulty in factorizing a large prime number ensures that attacker cannot find in finite time the two primes (p & q) used to obtain n. This is strength of RSA.
Generate the private key
Private Key d is calculated from p, q, and e. For given n and e, there is unique number d.
Number d is the inverse of e modulo (p - 1)(q – 1). This means that d is the number less than (p - 1)(q - 1) such that when multiplied by e, it is equal to 1 modulo (p - 1)(q - 1).
This relationship is written mathematically as follows −
The Extended Euclidean Algorithm takes p, q, and e as input and gives d as output.
Example
An example of generating RSA Key pair is given below. (For ease of understanding, the primes p & q taken here are small values. Practically, these values are very high).
Let two primes be p = 7 and q = 13. Thus, modulus n = pq = 7 x 13 = 91.
Select e = 5, which is a valid choice since there is no number that is common factor of 5 and (p − 1)(q − 1) = 6 × 12 = 72, except for 1.
The pair of numbers (n, e) = (91, 5) forms the public key and can be made available to anyone whom we wish to be able to send us encrypted messages.
Input p = 7, q = 13, and e = 5 to the Extended Euclidean Algorithm. The output will be d = 29.
Check that the d calculated is correct by computing −
Hence, public key is (91, 5) and private keys is (91, 29).
Encryption and Decryption
Once the key pair has been generated, the process of encryption and decryption are relatively straightforward and computationally easy.
Interestingly, RSA does not directly operate on strings of bits as in case of symmetric key encryption. It operates on numbers modulo n. Hence, it is necessary to represent the plaintext as a series of numbers less than n.
RSA Encryption
Suppose the sender wish to send some text message to someone whose public key is (n, e).
The sender then represents the plaintext as a series of numbers less than n.
To encrypt the first plaintext P, which is a number modulo n. The encryption process is simple mathematical step as −
In other words, the ciphertext C is equal to the plaintext P multiplied by itself e times and then reduced modulo n. This means that C is also a number less than n.
Returning to our Key Generation example with plaintext P = 10, we get ciphertext C −
RSA Decryption
The decryption process for RSA is also very straightforward. Suppose that the receiver of public-key pair (n, e) has received a ciphertext C.
Receiver raises C to the power of his private key d. The result modulo n will be the plaintext P.
Returning again to our numerical example, the ciphertext C = 82 would get decrypted to number 10 using private key 29 −
RSA Analysis
The security of RSA depends on the strengths of two separate functions. The RSA cryptosystem is most popular public-key cryptosystem strength of which is based on the practical difficulty of factoring the very large numbers.
Encryption Function − It is considered as a one-way function of converting plaintext into ciphertext and it can be reversed only with the knowledge of private key d.
Key Generation − The difficulty of determining a private key from an RSA public key is equivalent to factoring the modulus n. An attacker thus cannot use knowledge of an RSA public key to determine an RSA private key unless he can factor n. It is also a one way function, going from p & q values to modulus n is easy but reverse is not possible.
If either of these two functions are proved non one-way, then RSA will be broken. In fact, if a technique for factoring efficiently is developed then RSA will no longer be safe.
The strength of RSA encryption drastically goes down against attacks if the number p and q are not large primes and/ or chosen public key e is a small number.
ElGamal Cryptosystem
Along with RSA, there are other public-key cryptosystems proposed. Many of them are based on different versions of the Discrete Logarithm Problem.
ElGamal cryptosystem, called Elliptic Curve Variant, is based on the Discrete Logarithm Problem. It derives the strength from the assumption that the discrete logarithms cannot be found in practical time frame for a given number, while the inverse operation of the power can be computed efficiently.
Let us go through a simple version of ElGamal that works with numbers modulo p. In the case of elliptic curve variants, it is based on quite different number systems.
Generation of ElGamal Key Pair
Each user of ElGamal cryptosystem generates the key pair through as follows −
Choosing a large prime p. Generally a prime number of 1024 to 2048 bits length is chosen.
Choosing a generator element g.
This number must be between 1 and p − 1, but cannot be any number.
It is a generator of the multiplicative group of integers modulo p. This means for every integer m co-prime to p, there is an integer k such that gk=a mod n.
For example, 3 is generator of group 5 (Z5 Free vista product key generator. = {1, 2, 3, 4}).
| N | 3n | 3n mod 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
Choosing the private key. The private key x is any number bigger than 1 and smaller than p−1.
Computing part of the public key. The value y is computed from the parameters p, g and the private key x as follows −
Obtaining Public key. The ElGamal public key consists of the three parameters (p, g, y).
For example, suppose that p = 17 and that g = 6 (It can be confirmed that 6 is a generator of group Z17). The private key x can be any number bigger than 1 and smaller than 71, so we choose x = 5. The value y is then computed as follows −
Thus the private key is 62 and the public key is (17, 6, 7).
Encryption and Decryption
The generation of an ElGamal key pair is comparatively simpler than the equivalent process for RSA. But the encryption and decryption are slightly more complex than RSA.
ElGamal Encryption
Suppose sender wishes to send a plaintext to someone whose ElGamal public key is (p, g, y), then −
Sender represents the plaintext as a series of numbers modulo p.
To encrypt the first plaintext P, which is represented as a number modulo p. The encryption process to obtain the ciphertext C is as follows −
- Randomly generate a number k;
- Compute two values C1 and C2, where −
Send the ciphertext C, consisting of the two separate values (C1, C2), sent together.
Referring to our ElGamal key generation example given above, the plaintext P = 13 is encrypted as follows −
- Randomly generate a number, say k = 10
- Compute the two values C1 and C2, where −
Send the ciphertext C = (C1, C2) = (15, 9).
Generate Encryption Key With Diffie Hellman Windows 10
ElGamal Decryption
To decrypt the ciphertext (C1, C2) using private key x, the following two steps are taken −
Compute the modular inverse of (C1)x modulo p, which is (C1)-x , generally referred to as decryption factor.
Obtain the plaintext by using the following formula −
In our example, to decrypt the ciphertext C = (C1, C2) = (15, 9) using private key x = 5, the decryption factor is
Extract plaintext P = (9 × 9) mod 17 = 13.
ElGamal Analysis
In ElGamal system, each user has a private key x. and has three components of public key − prime modulus p, generator g, and public Y = gx mod p. The strength of the ElGamal is based on the difficulty of discrete logarithm problem.
The secure key size is generally > 1024 bits. Today even 2048 bits long key are used. On the processing speed front, Elgamal is quite slow, it is used mainly for key authentication protocols. Due to higher processing efficiency, Elliptic Curve variants of ElGamal are becoming increasingly popular.
Generate Encryption Key With Diffie Hellman Texas
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) is a term used to describe a suite of cryptographic tools and protocols whose security is based on special versions of the discrete logarithm problem. It does not use numbers modulo p.
ECC is based on sets of numbers that are associated with mathematical objects called elliptic curves. There are rules for adding and computing multiples of these numbers, just as there are for numbers modulo p.
ECC includes a variants of many cryptographic schemes that were initially designed for modular numbers such as ElGamal encryption and Digital Signature Algorithm.
It is believed that the discrete logarithm problem is much harder when applied to points on an elliptic curve. This prompts switching from numbers modulo p to points on an elliptic curve. Also an equivalent security level can be obtained with shorter keys if we use elliptic curve-based variants.
The shorter keys result in two benefits −
- Ease of key management
- Efficient computation
Generate Encryption Key With Diffie Hellman Free
These benefits make elliptic-curve-based variants of encryption scheme highly attractive for application where computing resources are constrained.
Wireshark Diffie Hellman
RSA and ElGamal Schemes – A Comparison
Generate Encryption Key With Diffie Hellman Lyrics
Let us briefly compare the RSA and ElGamal schemes on the various aspects.
Openssl Diffie Hellman
| RSA | ElGamal |
|---|---|
| It is more efficient for encryption. | It is more efficient for decryption. |
| It is less efficient for decryption. | It is more efficient for decryption. |
| For a particular security level, lengthy keys are required in RSA. | For the same level of security, very short keys are required. |
| It is widely accepted and used. | It is new and not very popular in market. |